In this article (and video above), we tackle a key concept from the Engineering Economics section of the FE Exam: PW Problems analysis. We’re given an investment with an initial cost and varying cash inflows over six years, and we calculate its value using an 8% interest rate. To do this, we apply the Single Payment Present Worth formula, which is ideal for handling non-uniform cash flows. Mastering this method is essential, as it’s a common topic you can expect to encounter on the FE Exam.
Question:
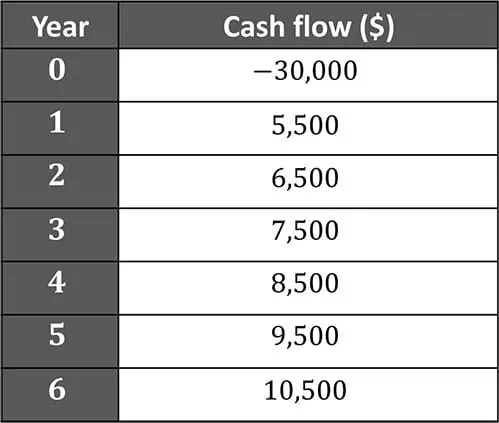
An investment generates the following cash flows over a 6-year period. Determine the Present Worth (PW) of the investment using an annual interest rate of 8%.
In today’s question, we are presented with a series of cash flows occurring over the span of 6 years. The investment has an initial cost of $30,000 in year zero, followed by a series of positive cash flows. Here, the goal is to calculate the Present Worth (PW) of these cash flows at an 8% interest rate. However, since these cash flows occur at different points in time, we’ll also need to account for the time value of money. Let’s start with a basic review of the concepts behind this problem:
The Present Worth Method:
The Present Worth method is a tool in engineering economics used to evaluate the total value of a series of future cash flows as if they occurred at the present time.
Time Value of Money:
[Read more…] about How to Solve PW Problems with Uneven Cash Flows