In this article (and video above), we tackle a key structural engineering topic from the FE Exam: bending moment calculation for a loaded 20-foot beam. Using mathematical models and real-world examples, we walk through the bending moment calculations and discuss their significance in structural design. Whether you’re a student or a professional engineer, this article and video will help you strengthen your understanding of fundamental structural principles for the FE Exam.
Question:
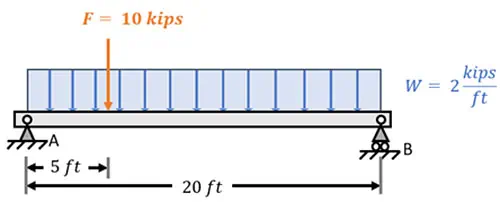
A simply supported beam with a span of 20 feet is subjected to two loadings. A concentrated point load of 10 kips is applied 5 feet from the left support (point A), and a uniformly distributed load of 2 kips/ft acts continuously along the entire length of the beam. Determine the maximum bending moment in the beam using a bending moment calculation.
In today’s problem, we are tasked with analyzing a \(20\,\text{ft}\) long simply supported beam subjected to both a point load and a uniformly distributed load. The point load is applied at a distance of \(5\,\text{ft}\) from support \(A\), while the uniformly distributed load of \(2\,\text{kips/ft}\) is applied across the entire span of the beam. Our goal is to determine the maximum bending moment in the beam and its location.
Explanation:
In today’s problem, we are tasked with analysing a 20 ft long simply supported beam subjected to both a point load and a uniformly distributed load. The point load is applied at a distance of 5 ft from support A, while the uniformly distributed load of 2 kips/ft is applied across the entire span of the beam. Our goal is to perform a bending moment calculation to determine the maximum bending moment in the beam and its location.
To find the maximum moment in the beam due to the applied loads, we first need to determine the beam’s reactions at its supports. We label these loads R_A and R_B respectively. For convenience, we can also label our applied point load as F and the distributed loading as W.
With all the forces accounted for, we can move on to applying the equations of static equilibrium. These equations are based on the fundamental principle that the sum of the vertical forces in a system must equal zero, and the sum of the moments about any point in the system must also equal zero.
\(\sum F_y = 0\)
\(\sum M_{A,B} = 0\)
Let’s find an equivalent load for the distributed force so we can apply this first equation. The total load intensity from the distributed load is calculated as the intensity of the load, \(2\,\text{kips/ft}\), multiplied by the beam’s length \(20\,\text{ft}\). This gives us an equivalent load of \(40\,\text{kips}\).
\(F_w = R_A \cdot L\)
\(F_w = 40\,\text{kips}\)
This represents the total load if the distributed loading were concentrated at the center of the beam as a single point load.
[Read more…] about How to Perform a Bending Moment Calculation for the FE Exam